Variable Expressions Part 3

Variable Expressions With More Than One Variable

                                            1

Once students have an understanding of variable expressions they will expand their knowledge by learning how and when terms in an expression can be combined.  Last term in Special Education I observed a student in math class.  I remember the lesson on combining like terms.  I remember the teachers explanation of how we can't add apples and oranges together.  Most of the students understood, but there were still several that questioned exactly what they were doing and why.  Having a solid understanding of this concept will help students when they move on to solving algebraic equations.

Word Wall

Like Terms - Terms where the variables and their exponents are the

                      same.

                          4x and 15x           -8y and 90y       5ab and 87ab

Combine Like Terms - The mathematical operation of adding or 

                      subtracting like terms.

Commutative Property of Addition - Changing the order of the operation does not change the answer.  example:  a + b = b + a

Simplify Like Terms

Students need to understand that variables are a representation for an unknown quantity.  It is easy for them to see that the variable x is different from the variable y, and simple enough to explain to them that they are different and therefore they can not be added together.  What happens when they see x and xy, or x²?  They still need to understand that those variables are different and can not be combined.  

Example:  Take x, xy, and x², because the variables can have different values they cannot be seen as similar or like, and added together.  If we say x = 4, then we would have 4, 4y, and 16.

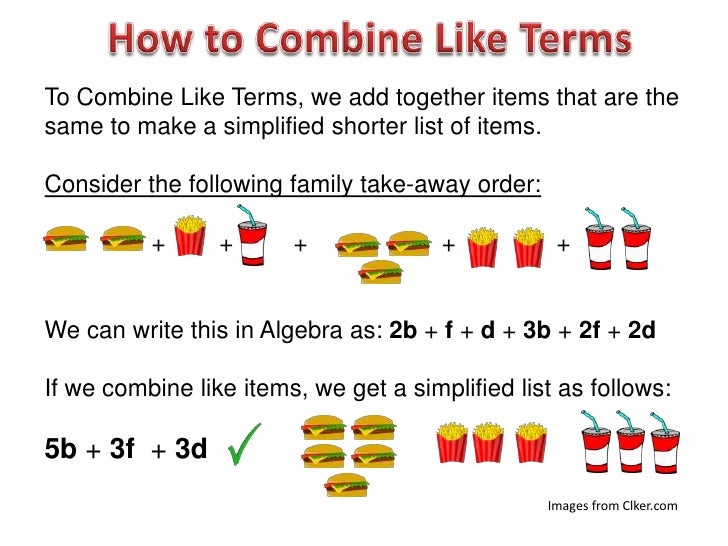
Some students could say that apples and oranges are both fruit, so why can't they be combined?  I found this slide presentation on LinkedIn Learning SlideShare.  I liked the way they presented the topic.  I think students can relate to this idea and could easily be to changed to reflect the classes interests.

²
²

How to Combine Like Terms

• When given an algebraic expression, students should evaluate what is in the expression.

         1.  5x + 2x            2.  10b - 5c + 2b            3.  10x² + 5x - 3x²  - 7x

• Then they can rewrite the expression by grouping the like terms together.  They can do this because of the commutative property of addition.

         1.  5x + 2x            2.  10b + 2b - 5c            3.  10x²  - 3x²  - 7x  + 5x

• Finally, add or subtract the like terms, simplifying the expression. 

         1.  5x + 2x = 7x       2.  10b + 2b - 5c = 12b - 5c      3.  10x²  - 3x²  - 7x  + 5x =
                                                                                                               7x² -7x

Conclusion

I like the idea of using an example that the students can relate to.  I believe with this approach, high-level word problems could be given to the students and they could set them up and solve them without much difficulty.  The problem that I see happening next is working with adding and subtracting positive and negative integers.  Students have a hard time remembering the rules of when to add and what to subtract.  Hopefully, once they understand when terms can be combined, they will be able to regroup.  We'll practice the rules of working with positive and negative terms next.

Sources

1 - https://imgflip.com/i/1pjnd7

2 - https://www.slideshare.net/bigpassy/combining-algebra-like-terms

Algebra Tiles

Algebra Tiles

I am looking for ways to teach algebra concepts to students and still keep it fun and interesting.  From what I have observed in 6th grade math class, they lose a lot of the freedom that they had in the lower elementary grades.  I've also noticed that they lose the manipulatives that help them to make a deeper connection and understanding to the ideas behind the work.  So, in my research, I found algebra tiles.  The more I read about them, the more I wanted to know how they can be used in a 6th grade mathematics classroom.  So, here's a guide on how to use algebra tiles.

What are algebra tiles?

Algebra tiles are manipulatives that model algebraic operations.  

The yellow tile represents a +1

The red tile represents a -1

A combination of the two tiles are additive inverses and would cancel each other out.

The green rectangle represents the variable

The red rectangle represents the negative variable

             The combination of these two tiles are inverses also and they would cancel each other out.

The third shape is a set of larger squares.  I'll explain what they represent because they are included in a set of tiles, but I wouldn't need them for the mathematics that I would be teaching.

       

       The large blue and red squares represent perfect squares.

        The blue square tile is x² and the red square tile is -x².

        Again, they are inverse operations.

How to use the tiles

• The single square tiles can be used like counting chips to model addition, subtraction, multiplication and division of integers.  
• Model algebraic expressions
• Model and solve algebraic equations
• Model the distributive property with a variable
• Model substitution with a variable
• Model polynomials using x²

Internet Resources

IXL:  https://www.ixl.com/math/grade-6/model-and-solve-equations-using-algebra-tiles

National Council of Teachers of Mathematics:

 https://www.nctm.org/Classroom-Resources/Illuminations/Interactives/Algebra-Tiles/

Make your own tiles

There are plenty of companies that sell algebra tiles, but you can make your own.  There are ideas and templates available.  You can also customize the tiles and write 1, -1 and x on the tiles instead of remembering the meaning of the colors.  They can be made from card stock or 3 x 5 cards.  It might be a good project for students to make their own set.  Then they can have them whenever they need them or when a new concept is being taught.  

I saw a suggestion to make a large set that would adhere to a whiteboard.  Make them magnetic if you have a surface to work on.

Common Core Standard

CCLS - Math:  6.EE.2.c

Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole- number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations).¹

Conclusion

Who would have thought that I would be excited about algebra tiles?  I would like to keep math fun and interesting beyond fourth grade.  From what I've seen, these types of strategies and supports are not used in 6th grade.  I like the way that mathematical ideas are being taught now.  I wasn't taught this way, but I wish I had been.  I really like the student centered approach and think I would have flourished in a math class that gave me a visual, hands-on way to learn the operations.

Sources

https://www.engageny.org/ccls-math/6ee2c

Variable Expressions Part 2

Variable Expressions

                                     ¹

Now that students have an understanding of algebra and the language involved we can look at understanding how to work with a variable expression.

An algebraic expression is a combination of numbers and variables together with at least one mathematical operation.
Examples:    x + 7   
               
                     8f - 6

                     7y + 2

Khan Academy

I am not a huge fan of Khan Academy.  I think they do good work, it's more of a personal thing.  Sal Kahn's voice gets to me and the way he tends to work back and forth bothers me after a while too. However, they have accumulated a great library of mathematical lessons that are relevant and informative.  I think I would ask my class if they find Khan Academy helpful before I started using them consistently.  If other students are affected by Mr. Kahn's mannerisms like I am then there is no point in showing several important ideas presented by Khan Academy.

Why all the letters in algebra?

https://www.khanacademy.org/math/algebra/introduction-to-algebra/overview-hist-alg/v/why-all-the-letters-in-algebra

This video is short, 3:03, and gives a brief explanation of why we use letters in algebra.  It seems harmless enough and I'd use it to start this lesson.

Why aren't we using a multiplication sign?  (4:57)

https://www.khanacademy.org/math/algebra/introduction-to-algebra/alg1-intro-to-variables/v/why-aren-t-we-using-the-multiplication-sign

This video explains why we don't use a multiplication sign when using variables.  It's a very important topic that students must understand in order to be able to "read" algebraic expressions.  We do a lot of multiplying in algebra and the letter X is a popular variable.  The expression 2 x X + 9 looks crazy and would be very difficult to figure out.
The video explains that we have several ways to show multiplication at this point in our mathematical learning:

     5 * x, in this case the dot is the symbol for multiplication. 
   
     5 (x), in this case the parentheses show multiplication.
   
     5 x, we can remove the parentheses and place the 5 next to the x, 5x,  because it is easy to see that the two items are different and do not go together.  Students would need to learn that when they see 5x or any number sitting next to a variable the operation between them is multiplication.  This will be important later when we need to move, or undo, that 5 coefficient from the x variable. 

Evaluating Variable Expressions

To begin working with variable expressions we need one more word for our word wall.

Substitution - The act of replacing one thing with another thing.  
         * In this case we will replace the variable (letter) with a number.

How do we begin?  When we have an expression given to us, and we are asked to evaluate that expression, we are normally give the number that we are going to use.  Take a look at the example:

Evaluate the expression below, where Y = 3:

Y + 7:  Students should understand that Y is the variable and 7 is a constant. 

They are asked to evaluate the expression if Y = 3.
The next step would be to substitute the 3 for the Y in the expression.    3 + 7
Then do the math.  3 + 7 = 10

This lesson would probably continue with a few more examples, either with the class, in small groups or individual work and then a worksheet could be added so they could practice what they learned.  However, I found algebra tiles in my research for this topic!  The next great step in understanding this concept would allow the students time to work with a manipulative and hopefully help to make these ideas more concrete. 

Manipulative Help

I love the idea of algebra tiles.  They remind me of the previous work that most students will have done with base ten blocks and ten frames.  Algebra tiles are a tactile way of helping with algebraic manipulation. 

 

This set of tiles contains red and green rectangles and red and yellow squares.  The rectangles represent the variable and the small squares represent the constant or the number.  The color red represents a negative number.  The green rectangle is a positive variable and the yellow square is a positive number. 

Video:  Learn to evaluate expressions using algebra tiles

https://www.youtube.com/watch?v=f2o8EI0iOYg

The video is 7:01 in length.  It demonstrates how to use the tiles.  At 4:13, they explain how to model algebraic expressions and solve for the variable. 

Algebra tiles would be a great way for students to practice working with variable expressions.  Once they have mastered the objective in a visual, tactile way, they are ready to move to paper.  Students who feel they have mastered the concept can work on a standard worksheet.  Those that aren't ready to leave the shapes and colors completely, can work with a modified worksheet that provides them the familiar help they need.  It is also possible for yet another group of students to complete the worksheet while still using the algebra tiles.

Common Core Standard

CCLS - Math:  6.EE.2.c

Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole- number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations).²

Conclusion

Wow!  I feel like I didn't really get anywhere with this, but I made a few discoveries.  I have a better understanding about how difficult it is to break down an idea into manageable chunks for young learners to understand.  I can see there are a lot of resource available, but you need time to sort through them to make sure they are appropriate for your students and helping to advance the lesson in the way that you want it to go.  I can understand not that it would be easy to lose track of the mathematical objectives as you sort through all the information.  I am really impressed with the algebra tiles and think I'll devote the next blog to them.  I'll pick up with variable expressions after I explore how helpful the tiles will be for young learners.   

Sources

1 - http://www.mathfunny.com/images/mathpics-mathjoke-haha-humor-pun-mathmeme-meme-joke-math-problems-harry-variable-equation-xyz.jpg

2 - https://www.engageny.org/ccls-math/6ee2c

Variable Expressions

How To Introduce The Idea Of A Variable In An Algebraic Expression

I have a better understanding of what it takes to help students develop number sense in their early years of elementary school.  So, when we start to give them algebraic ideas in 6th grade, we are asking them to take their concrete knowledge and apply it to a conceptual idea, what is the value of x?

Word Wall

Start a word wall with vocabulary specific to algebra.  Math has its own language.  It's important for students to continue to add to their mathematical vocabulary in order to be successful in math.

Algebra - A branch of mathematics that introduces symbols for unknown quantities and rules for how to manipulate those quantities.¹ 

Variable - A symbol used in algebra to represent a quantity without a fixed value.¹    x    y    b    c   

Constant - A number on its own.²   6    20    74       

Coefficient - A number multiplied to a variable²

4x    10x   3y   18y

Algebraic Term - A number or a variable, or a number and variable multiplied together²

Operation - Mathematical manipulation, doing something with the values.²  
Addition (+) , Subtraction (-), Multiplication (x), or Division (÷)

Algebraic Expression - A group of terms separated by an operation, +, or -.²      6x + 5 

* Things to consider as you teach this concept.  Students will be comfortable using the symbol X to indicate the operation of multiplication.  They need to learn they will no longer want to use the X when they are learning algebra.  The symbol is commonly used as a variable, an unknown quantity.  To see the expression, 3 x X, will not make any sense to them.  They will need to make the transition from the X symbol to a dot, *, to the idea that 3x is 3 multiplied by x.   (Sorry, I could not find a solid dot to use.)

Videos

Using videos as another source of information helps students understand the concepts they need to learn in advance.  Typically a video shows an entire sequence of steps and mathematical manipulations.  It provides a overview of an idea or concept.  Students have the opportunity to see where they are going. Videos offer the ideas your about to teach in a visual way and if helps if their at that point in the year where they can tune out your voice.

What is Algebra?  (2:37)

https://www.youtube.com/watch?v=5Q0FlxcEEIw

Brain Pop

-Our elementary school pays for a subscription to the website BrainPop.  It is an educational site with animated videos in the core subjects, English, math, social studies and science, and several more.  The main characters Tim and Moby, answer letters sent in by students with questions they have on a subject.  They offer movies,quizzes, activities, concept maps and games.  

Here's a BrainPop webinar:  https://educators.brainpop.com/video/brainpop-overview-2018/  (37:41) 

Equations with Variables 

https://www.brainpop.com/math/algebra/equationswithvariables/

Tim and Moby use a one-variable equation to help build a ladder to get to their tree house.  They cover ideas like, substituting numbers for letters and isolating a variable.

Common Core Standard

CCLS - Math: 6.EE.2.c

Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole- number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations).³

Conclusion

When I started to break down the concepts in this lesson, I realized the amount of information that students need to understand before they can actually work with an algebraic expression.  The vocabulary alone is a lot to handle.  I believe working with the vocabulary and becoming familiar with the terms will help to minimize confusion when they start using variable terms and operations.  I think once I've gone over the vocabulary and we created our word wall, students should write the vocabulary words and definitions in their notes and make up their own examples.  When they are finished we could practice comprehension with individual whiteboards and dry erase markers as a class.  I would read them a vocabulary word and they would write an example of it on the dry erase board, show it me so I can see that they understand the word, its meaning and how to represent it.


Sources:

1 - https://www.livescience.com/50258-algebra.html

2 - https://www.mathsisfun.com/algebra/definitions.html

3 - https://www.engageny.org/ccls-math/6ee2c