Fact Families, Number Lines, and Games

Positive and Negative Numbers:  

Fact Families, Number Lines, and Games

While researching the operation rules for positive and negative numbers, I came across the term fact families.  I looked it up and learned that it is a group of numbers used to demonstrate a mathematical principle.  Fact Families are used as a strategy in early elementary mathematics to make math easier to understand for students in first through third grade.  They build on a foundation of mathematical facts that the student already knows to be true.  

Fact Families

Fact families are introduced as a strategy for students to help them with addition and subtraction, then multiplication and division.  They begin with 3 numbers that can be represented in 4 different mathematical equations that are all true.  The numbers in the family either add or subtract to equal each other.  Students need to check their work to make sure that the fact belongs to the fact family.  Using fact families helps students fill in the blanks and make connections between the numbers.  They get comfortable manipulating numbers forwards and backwards, doing and undoing operations.  They are working with inverse operations with ease.
For example,  let's look at the fact family of 4, 5, and 9.
Students should be able to write 4 facts that are true statements about how these numbers relate to each other in terms of addition and subtraction.
                                                     4, 5, 9

                                            1.  4 + 5 = 9
                                2.  5 + 4 = 9
  *  After writing the two addition statements, students should take the sum and write two subtraction statements with numbers from the fact family.                          
                                    3.  9 - 5 = 4
                                            4.  9 - 4 = 5 

     *  They can continue by recognizing the statements that do not belong in the fact family.  While these statements are true, they do not help students connect the addition to the subtraction, therefore, they are not part of the fact family.

                                           5.  9 + 4 = 13
                                           6.  9 + 5 = 14  

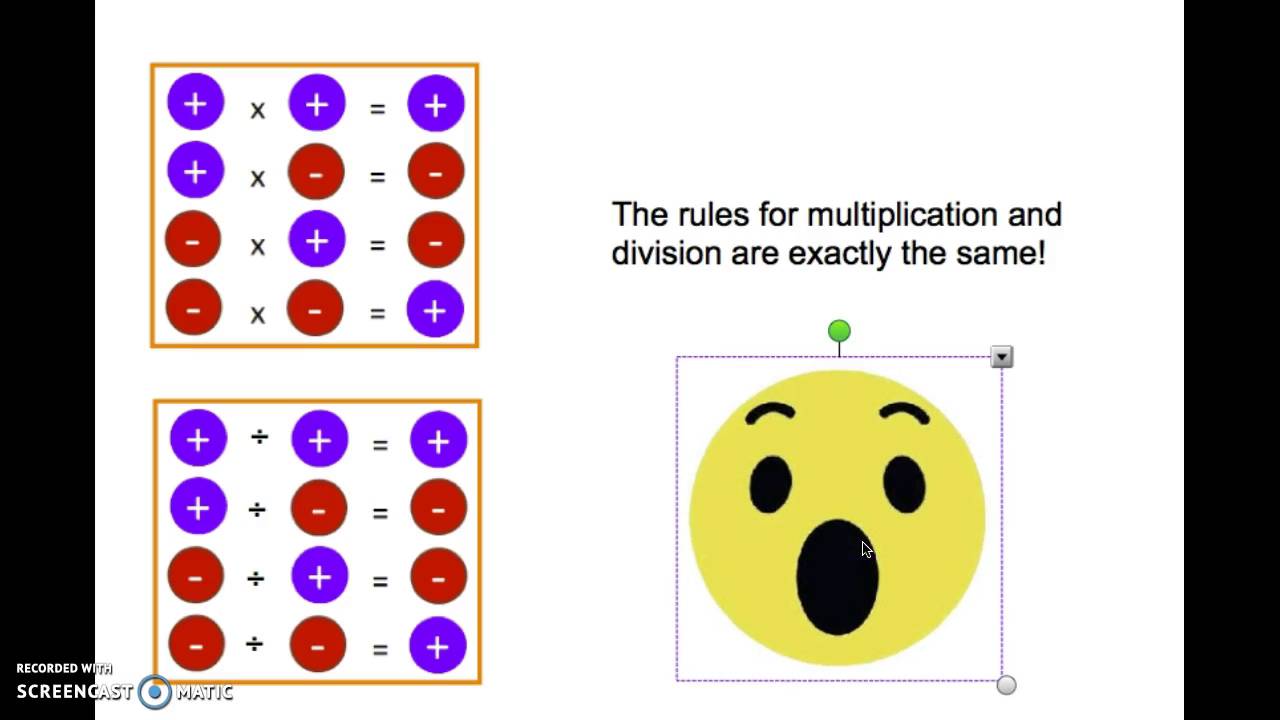
Fact families work with positive and negative numbers.  If students are familiar with fact families from their early elementary math classes, introduce them as a strategy to understand the manipulation of positive and negative numbers.

    3, -4, -7                         -2, -3, -5

     Addition:          3 + -7 = -4                       -2 + -3 = -5

     Addition:          -7 + 3 = -4                       -3 + -2 = -5

     Subtraction:      -4 - 3 = -7                      -5 - (-2) = -3 

     Subtraction:    -4 - (-7) = 3                      -5 - (-3) = -2       

Number Lines

¹

Number Lines help students understand negative numbers by giving them a point of reference, a visual representation of a negative number.  Students aren't really taught about negative numbers until 6th grade.  They may have seen a science problem with negative degrees on a thermometer or heard that as you go further below sea level, you use negative numbers, but they do not use them in mathematical operations until 6th grade. Number lines are a great way to introduce negative numbers and their relationship to positive numbers.

Games   

To recognize the importance of games and learning math, I found a website hosted by the University of Cambridge and their NRICH Maths project.  The project is aimed at enriching mathematics for all math learners and to provide high-level engaging materials for teachers to use in their classrooms.   

Their game, Tug Harder!, involves playing a game along a positive and negative number line.

²

 First Connect Three is another one of their games using positive and negative numbers:

²

Visit their website for more game options.  They have resources for teachers and students.

 https://nrich.maths.org/

Common Core Standards³

CCSS.MATH.CONTENT.6.NS.C.5

CCSS.MATH.CONTENT.6.NS.C.6

CCSS.MATH.CONTENT.6.NS.C.6.A

Conclusion

Students need to learn how to work with positive and negative numbers.  These numbers have specific rules for each mathematical operation, and learning these rules will help make the life of a young mathematician so much easier.  Students might have to memorize the rules, but there are many ways to support students as they learn the rules.  Teachers should invest a little more time on this subject, hang posters in their rooms, use manipulatives, show videos and play games with their students.  I think this practice is the foundation for a major portion of  the mathematics curriculum going forward after 6th grade.     

Sources:

1- http://www.11plusforparents.co.uk/Maths/negativenum.html

2 - https://nrich.maths.org/5898

3 - http://www.corestandards.org/Math/Content/6/NS/

Multiplying and Dividing Positive and Negative Numbers

Continuing the Rules for Positive and Negative Numbers:

Multiplying and Dividing 

I wanted to continue with the rules for positive and negative numbers because the rules for adding and subtracting were tricky.   
Fortunately, the rules for multiplying and dividing are a little easier and after working with addition and subtraction hopefully students think so too.

Word Wall

In my research this week I can across the term fact family.  I liked what I learned about it because it reminded me of previous examples we've seen where the teacher selects specific numbers to teach a lesson.  Fact Family falls into this concept.  The fact family helps us understand the relationship between operations.  I'll delve deeper into this concept in my next blog.

Fact Family:  A group of math facts or equations using the same set of numbers.    

Multiplication Rules

1)  A positive times a positive equals a positive
                            5 x 5 = 25

2)  A negative times a negative equals a negative
                          -4 x -4 = 16

3)  A positive times a negative equals a negative
                          5 x -4 = -20

4)  A negative times a positive equals a negative
                          -5 x 4 = -20 

Division Rules

The rules for division are the same as the rules for multiplication.

₁

Flocabulary

Our social study teachers show the Flocabulary Week in Rap every Friday.  The students love it!  They use hip-hop rhythms and rap lyrics to get students excited about learning.  I had no idea they covered every subject and had lessons that aligned with state standards.  You have to pay for the service.  The attached video is 3:18 in length, but I don't have an account it only shows the first :40 seconds, you'll get a feel for what they do though.       

https://www.flocabulary.com/unit/multiplying-dividing-integers/  (3:18)

Poster

This poster demonstrates the rules for all of the operations.

²

Conclusion

It is so important that students learn these rules.  Teachers need to demonstrate then in several ways to their students so they really grasp them.  They need to hear them, see them and use them in order to really understand them.  I'd recommend using manipulatives like chips or the - and + spacers we learned about in class.  Find interesting videos on the topic and allow students to work together to reason out why these rules work the way they do.  Also, have students apply them to real world problems to so they can connect meaning to them. 

Sources:

1 - https://www.youtube.com/watch?v=L1ZNw8Antv8

2 - http://www.loisterms.com/lois21.htm

Adding and Subtracting Positive and Negative Integers

¹

Rules for Adding and Subtracting Positive and Negative Numbers 

     Students come into sixth grade knowing what numbers are and many way to work with them.  Now they are asked to recognize a letter as a number and a number with a negative sign in front of it.  They will work extensively with positive and negative numbers during their sixth grade year and the better they feel about them going into 7th grade they better they will do.  There are specific rules for each operation with these numbers.  How can math teachers help students conceptualize the rules of positive and negative numbers so that they can be successful as they move on in math? 

Word Wall

Integers:  The set of whole numbers.  They can be positive, negative and zero.  No fractions.

Rational Numbers: A set of numbers that can be written as a  fraction or a whole number.  The quotient of the fraction either ends or repeats in a pattern. 

Negative Number:  A number less than zero

Positive Number:  A number greater then zero

Zero:  The number between the set of negative numbers and the set of positive numbers.  Zero is neither positive or negative. 

Absolute Value:  The distance from zero on the number line.  The absolute value is always positive. 

Positive and Negative Number Rules

There are 3 rules for addition:

1)  Adding two positive numbers, add and keep the sign.
                             6 + 3 = 9

2)  Adding two negative numbers, add and keep the sign.

                             -6 + -3 = -9

3)  When adding a positive number and a negative number, subtract the numbers and keep the sign of number with the largest absolute value.                  -6 + 3 = -3

Subtraction:

1)  Subtracting two positive numbers is simple subtraction.
                                    7 - 4 = 3

2)  Subtracting a positive number from a negative number, change the subtraction to addition and change the number from positive to negative and add.        -7 - 4
                                    -7 + (-4) = -11

3)  Subtracting a negative number:    7 - (-4) 
     Two negatives make a positive:    7 + 4 = 11

Poster and Chip Models 

 ²         

The following video explains how to subtract integers using positive and negative chips.  I love this idea and would use it in the classroom.  It really helps to see the idea of zeroing out 

Subtracting Integers Using a Chip Model (5:55)

https://www.youtube.com/watch?v=_77vO0uzBfA

Chip Models are great manipulatives to use in a classroom to help solidify this idea.  They provide a practical way to see what is happening with the positive and negative numbers.  

 ³



Common Core Standards⁴

CCSS.MATH.CONTENT.6.NS.C.6
Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.

CCSS.MATH.CONTENT.6.NS.C.6.A
Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., -(-3) = 3, and that 0 is its own opposite.

Conclusion

These rules are so specific to mathematical operations, that students must know them if they are going to be successful in the classroom.  I think it is important for teachers to slow down at this point in their curriculum and pull out all the manipulatives and support they can find to help students get these rules down.  From what I've seen in middle school, 7th grade math teachers expect the students to already know the rules and spend very little time, if any, reviewing them.  I'd recommend displaying posters, have students make note cards, watch different video's and use the chip model.  Looking at the rules from different perspectives and practicing them will help students understand how they work.     

Sources:

1 - https://i.pinimg.com/originals/1d/0e/95/1d0e953c1db6411ac3d1a18e1d82f789.jpg

2 - https://www.pinterest.com/pin/418201515371741167/?lp=true

3 - https://www.slideshare.net/aeherzog/adding-integers-ppt-3331211

4 - http://www.corestandards.org/Math/Content/6/NS/

Translating Algebraic Expressions

     As students progress into algebra, they need to be able to understand and interpret algebraic expressions.  Even though the expressions are usually short and relatively simple to read, they can be tricky for students to translate.  Students need to remember their mathematical terms for each operation.  They also need to be aware of "stitch order" and the use of parenthesis.  

Vocabulary

Algebraic Phrase:  A short written statement that contains numbers, variables, and mathematical operations

Need To Know

Algebraic expressions are like short word problems. 

Recall all key operation vocabulary:  

¹  

                                                     

                                             

                

Study and Practice²

Flash Cards
To help students remember the key words they could make flash cards to study with.  

Using 3x5 index cards they would write the operation and its symbol (+, -, x, /) on the front of the card and the associated key terms on the back, lined side of the card.  They can study independently or with a partner.  It is important that they know these words to help them translate a phrase properly.  

"Math Coach"

Once students have a set of 3x5 cards, they can start translating algebraic expressions.  Students can work in groups practicing how to translate an algebraic phrase.  Have one student read a phrase aloud to the group.  Students should underline any key terms that they find. The "math coaches" in the group would use their flash cards to identify the vocabulary in the phrase and follow the flash card operation.  The group should switch readers and coaches after they translate each phrase.
 
Example:
1.)  Break the phrase up into sections:  three times a number plus twelve    

                                                   three times a number plus twelve

2.)  Translate the identified key words:    3 * x + 12    

3.)  Rewrite in a variable phrase:              3x + 12

Switch Order Example:  six taken away from 5 and a number

1.)  Identify                 six taken away from 5 and a number

2.)  Translate                             6      -       5x   
     *This order will not work.  Students need to recognize they need the 5x first before they can take 6 away.  

3.)  Switch Order                       5x-6                                                  

Common Core Standard ³

CCSS.Math.Content.6.EE.A.2
Write, read, and evaluate expressions in which letters stand for numbers.

CCSS.Math.Content.6.EE.A.2.a
Write expressions that record operations with numbers and with letters standing for numbers. For example, express the calculation "Subtract y from 5" as 5 - y.

Sources:

1 - https://img1.etsystatic.com/046/0/10046090/il_570xN.677510387_py3b.jpg

2 - https://www.vocabulary.com/articles/lessons/using-key-words-to-unlock-math-word-problems/

3 - http://www.corestandards.org/Math/Content/6/EE/

Variable Expressions Part 3

Variable Expressions With More Than One Variable

                                            1

Once students have an understanding of variable expressions they will expand their knowledge by learning how and when terms in an expression can be combined.  Last term in Special Education I observed a student in math class.  I remember the lesson on combining like terms.  I remember the teachers explanation of how we can't add apples and oranges together.  Most of the students understood, but there were still several that questioned exactly what they were doing and why.  Having a solid understanding of this concept will help students when they move on to solving algebraic equations.

Word Wall

Like Terms - Terms where the variables and their exponents are the

                      same.

                          4x and 15x           -8y and 90y       5ab and 87ab

Combine Like Terms - The mathematical operation of adding or 

                      subtracting like terms.

Commutative Property of Addition - Changing the order of the operation does not change the answer.  example:  a + b = b + a

Simplify Like Terms

Students need to understand that variables are a representation for an unknown quantity.  It is easy for them to see that the variable x is different from the variable y, and simple enough to explain to them that they are different and therefore they can not be added together.  What happens when they see x and xy, or x²?  They still need to understand that those variables are different and can not be combined.  

Example:  Take x, xy, and x², because the variables can have different values they cannot be seen as similar or like, and added together.  If we say x = 4, then we would have 4, 4y, and 16.

Some students could say that apples and oranges are both fruit, so why can't they be combined?  I found this slide presentation on LinkedIn Learning SlideShare.  I liked the way they presented the topic.  I think students can relate to this idea and could easily be to changed to reflect the classes interests.

²
²

How to Combine Like Terms

• When given an algebraic expression, students should evaluate what is in the expression.

         1.  5x + 2x            2.  10b - 5c + 2b            3.  10x² + 5x - 3x²  - 7x

• Then they can rewrite the expression by grouping the like terms together.  They can do this because of the commutative property of addition.

         1.  5x + 2x            2.  10b + 2b - 5c            3.  10x²  - 3x²  - 7x  + 5x

• Finally, add or subtract the like terms, simplifying the expression. 

         1.  5x + 2x = 7x       2.  10b + 2b - 5c = 12b - 5c      3.  10x²  - 3x²  - 7x  + 5x =
                                                                                                               7x² -7x

Conclusion

I like the idea of using an example that the students can relate to.  I believe with this approach, high-level word problems could be given to the students and they could set them up and solve them without much difficulty.  The problem that I see happening next is working with adding and subtracting positive and negative integers.  Students have a hard time remembering the rules of when to add and what to subtract.  Hopefully, once they understand when terms can be combined, they will be able to regroup.  We'll practice the rules of working with positive and negative terms next.

Sources

1 - https://imgflip.com/i/1pjnd7

2 - https://www.slideshare.net/bigpassy/combining-algebra-like-terms

Algebra Tiles

Algebra Tiles

I am looking for ways to teach algebra concepts to students and still keep it fun and interesting.  From what I have observed in 6th grade math class, they lose a lot of the freedom that they had in the lower elementary grades.  I've also noticed that they lose the manipulatives that help them to make a deeper connection and understanding to the ideas behind the work.  So, in my research, I found algebra tiles.  The more I read about them, the more I wanted to know how they can be used in a 6th grade mathematics classroom.  So, here's a guide on how to use algebra tiles.

What are algebra tiles?

Algebra tiles are manipulatives that model algebraic operations.  

The yellow tile represents a +1

The red tile represents a -1

A combination of the two tiles are additive inverses and would cancel each other out.

The green rectangle represents the variable

The red rectangle represents the negative variable

             The combination of these two tiles are inverses also and they would cancel each other out.

The third shape is a set of larger squares.  I'll explain what they represent because they are included in a set of tiles, but I wouldn't need them for the mathematics that I would be teaching.

       

       The large blue and red squares represent perfect squares.

        The blue square tile is x² and the red square tile is -x².

        Again, they are inverse operations.

How to use the tiles

• The single square tiles can be used like counting chips to model addition, subtraction, multiplication and division of integers.  
• Model algebraic expressions
• Model and solve algebraic equations
• Model the distributive property with a variable
• Model substitution with a variable
• Model polynomials using x²

Internet Resources

IXL:  https://www.ixl.com/math/grade-6/model-and-solve-equations-using-algebra-tiles

National Council of Teachers of Mathematics:

 https://www.nctm.org/Classroom-Resources/Illuminations/Interactives/Algebra-Tiles/

Make your own tiles

There are plenty of companies that sell algebra tiles, but you can make your own.  There are ideas and templates available.  You can also customize the tiles and write 1, -1 and x on the tiles instead of remembering the meaning of the colors.  They can be made from card stock or 3 x 5 cards.  It might be a good project for students to make their own set.  Then they can have them whenever they need them or when a new concept is being taught.  

I saw a suggestion to make a large set that would adhere to a whiteboard.  Make them magnetic if you have a surface to work on.

Common Core Standard

CCLS - Math:  6.EE.2.c

Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole- number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations).¹

Conclusion

Who would have thought that I would be excited about algebra tiles?  I would like to keep math fun and interesting beyond fourth grade.  From what I've seen, these types of strategies and supports are not used in 6th grade.  I like the way that mathematical ideas are being taught now.  I wasn't taught this way, but I wish I had been.  I really like the student centered approach and think I would have flourished in a math class that gave me a visual, hands-on way to learn the operations.

Sources

https://www.engageny.org/ccls-math/6ee2c

Variable Expressions Part 2

Variable Expressions

                                     ¹

Now that students have an understanding of algebra and the language involved we can look at understanding how to work with a variable expression.

An algebraic expression is a combination of numbers and variables together with at least one mathematical operation.
Examples:    x + 7   
               
                     8f - 6

                     7y + 2

Khan Academy

I am not a huge fan of Khan Academy.  I think they do good work, it's more of a personal thing.  Sal Kahn's voice gets to me and the way he tends to work back and forth bothers me after a while too. However, they have accumulated a great library of mathematical lessons that are relevant and informative.  I think I would ask my class if they find Khan Academy helpful before I started using them consistently.  If other students are affected by Mr. Kahn's mannerisms like I am then there is no point in showing several important ideas presented by Khan Academy.

Why all the letters in algebra?

https://www.khanacademy.org/math/algebra/introduction-to-algebra/overview-hist-alg/v/why-all-the-letters-in-algebra

This video is short, 3:03, and gives a brief explanation of why we use letters in algebra.  It seems harmless enough and I'd use it to start this lesson.

Why aren't we using a multiplication sign?  (4:57)

https://www.khanacademy.org/math/algebra/introduction-to-algebra/alg1-intro-to-variables/v/why-aren-t-we-using-the-multiplication-sign

This video explains why we don't use a multiplication sign when using variables.  It's a very important topic that students must understand in order to be able to "read" algebraic expressions.  We do a lot of multiplying in algebra and the letter X is a popular variable.  The expression 2 x X + 9 looks crazy and would be very difficult to figure out.
The video explains that we have several ways to show multiplication at this point in our mathematical learning:

     5 * x, in this case the dot is the symbol for multiplication. 
   
     5 (x), in this case the parentheses show multiplication.
   
     5 x, we can remove the parentheses and place the 5 next to the x, 5x,  because it is easy to see that the two items are different and do not go together.  Students would need to learn that when they see 5x or any number sitting next to a variable the operation between them is multiplication.  This will be important later when we need to move, or undo, that 5 coefficient from the x variable. 

Evaluating Variable Expressions

To begin working with variable expressions we need one more word for our word wall.

Substitution - The act of replacing one thing with another thing.  
         * In this case we will replace the variable (letter) with a number.

How do we begin?  When we have an expression given to us, and we are asked to evaluate that expression, we are normally give the number that we are going to use.  Take a look at the example:

Evaluate the expression below, where Y = 3:

Y + 7:  Students should understand that Y is the variable and 7 is a constant. 

They are asked to evaluate the expression if Y = 3.
The next step would be to substitute the 3 for the Y in the expression.    3 + 7
Then do the math.  3 + 7 = 10

This lesson would probably continue with a few more examples, either with the class, in small groups or individual work and then a worksheet could be added so they could practice what they learned.  However, I found algebra tiles in my research for this topic!  The next great step in understanding this concept would allow the students time to work with a manipulative and hopefully help to make these ideas more concrete. 

Manipulative Help

I love the idea of algebra tiles.  They remind me of the previous work that most students will have done with base ten blocks and ten frames.  Algebra tiles are a tactile way of helping with algebraic manipulation. 

 

This set of tiles contains red and green rectangles and red and yellow squares.  The rectangles represent the variable and the small squares represent the constant or the number.  The color red represents a negative number.  The green rectangle is a positive variable and the yellow square is a positive number. 

Video:  Learn to evaluate expressions using algebra tiles

https://www.youtube.com/watch?v=f2o8EI0iOYg

The video is 7:01 in length.  It demonstrates how to use the tiles.  At 4:13, they explain how to model algebraic expressions and solve for the variable. 

Algebra tiles would be a great way for students to practice working with variable expressions.  Once they have mastered the objective in a visual, tactile way, they are ready to move to paper.  Students who feel they have mastered the concept can work on a standard worksheet.  Those that aren't ready to leave the shapes and colors completely, can work with a modified worksheet that provides them the familiar help they need.  It is also possible for yet another group of students to complete the worksheet while still using the algebra tiles.

Common Core Standard

CCLS - Math:  6.EE.2.c

Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole- number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations).²

Conclusion

Wow!  I feel like I didn't really get anywhere with this, but I made a few discoveries.  I have a better understanding about how difficult it is to break down an idea into manageable chunks for young learners to understand.  I can see there are a lot of resource available, but you need time to sort through them to make sure they are appropriate for your students and helping to advance the lesson in the way that you want it to go.  I can understand not that it would be easy to lose track of the mathematical objectives as you sort through all the information.  I am really impressed with the algebra tiles and think I'll devote the next blog to them.  I'll pick up with variable expressions after I explore how helpful the tiles will be for young learners.   

Sources

1 - http://www.mathfunny.com/images/mathpics-mathjoke-haha-humor-pun-mathmeme-meme-joke-math-problems-harry-variable-equation-xyz.jpg

2 - https://www.engageny.org/ccls-math/6ee2c